Chapters
Mathematics For Machine Learning
Vectors & Matrices
Chapters
Introduction
Why Linear Algebra (or infact, Mathematics)?
Foundation of Machine Learning:
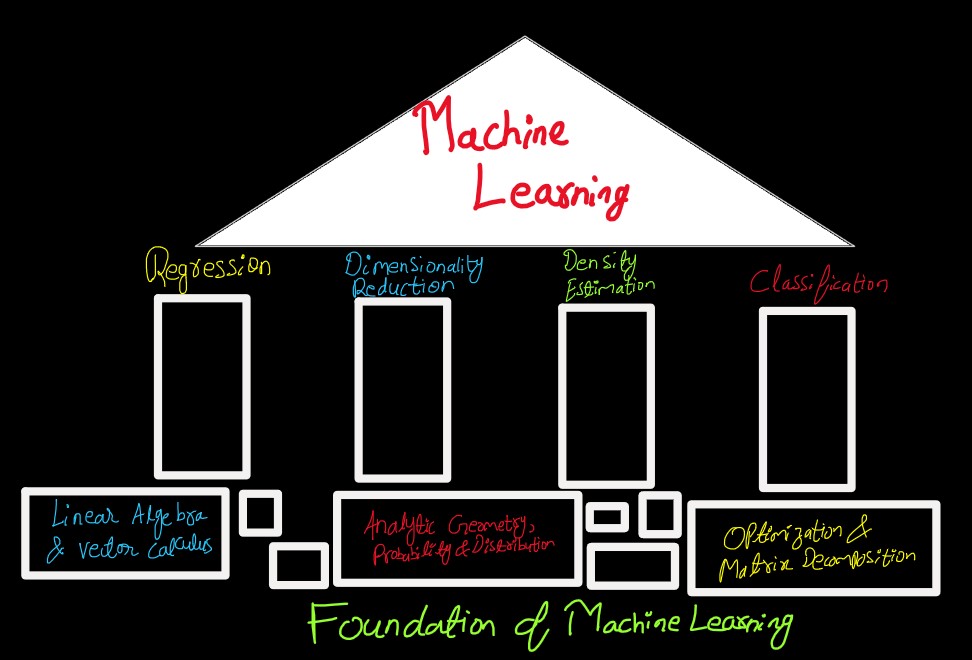 Credits: Mathematics for Machine
Learning
Credits: Mathematics for Machine
Learning
What are these blocks and how are they supporting Machine Learning?
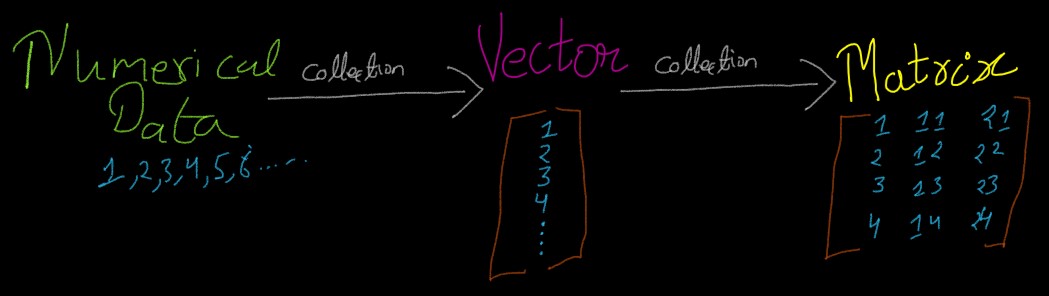
Machine Learning works on Data. We can represent data either in Natural Language
form, e.g. Words and alphabets, or we can
represent data in a Numerical form, i.e. numbers.
Collection of Numerical data can be represented as Vector, and a table of Vectors is
called as Matrix
And, the study of vectors and set of rules that can be applied to them in order to
manipulate them is called as Linear Algebra, one of the block in the bottom layer of
Machine Learning foundation figure.
When provided with 2 vectors or matrix, we often would want to learn about those 2 vectors or
matrices, i.e. to know what kind of realationship exsists between them. One way of knowing the
relationship between 2 such vectors or mtrices could be finding out about the similarity between
them. And Analytic Geometry (another supporting block from figure above) deals with the
study and finding out of similarities.
While working with Machine Learning, and making predictions, we often want to know of the
certanities or confidence of the predictions. Probability Theory helps to quantifiy the
uncertainity of Machine Learning's algorithms.
Machine Learning algorithms are trained to find solution via model training. Training is about
finding the right value of parameters that maximizes the performance measure. And many
optimization techniques
require the concept of a gradient, which tell us the direction in which to find the
optimal solution, i.e. optimized paramter or optimal cost function value. It is achieved using
Vector Calculus
 Credits: wikimedia.org
Credits: wikimedia.org
Moreover, to better understanding of a matrix, in terms of its intuitive interpretation, helps in various operations of machine learning, thus we need Matrix Decomposition for better interpretation of Matrices (and thus data) and more efficient learning.
Using all these foundation of mathematics, i.e. the lower part of the figure above, Machine Learning algorithms can be built and used to solve different kind of problems. One very common among all is Linear Regression, First Pillar in the diagram above. Linear Regression is a linear approach for modelling the relationship between a scalar response and one or more explanatory variable.
Other application can be Dimensionality Reduction,third pillar in the figure, to
find a compact, lower
dimensional representation of a high dimensional data, which makes it easier to analyze data.
Machine learning can also help in Density Estimation, fourth pillar in the figure, to
find a probability distribution that describes the given dataset.
Dimensionality Reduction & Density Estimation are both unsupervised learning i.e.
they don't have labels associated with the dataset. However in Density Estimation we're not
looking to achieve a lower
dimensional data representation, but a density model that describes data.
Linear Algebra
Algebra: When trying to work around intuition, it's common to make use of
symbols or set of symbols i.e. objects, and apply some rules to manipulate the objects.
This is known as Algebra
Linear Algebra: Study of vectors and set of rules that can be applied to manipulate them.
It provides a language to understand space, elements in a space, and
manipulation of space.
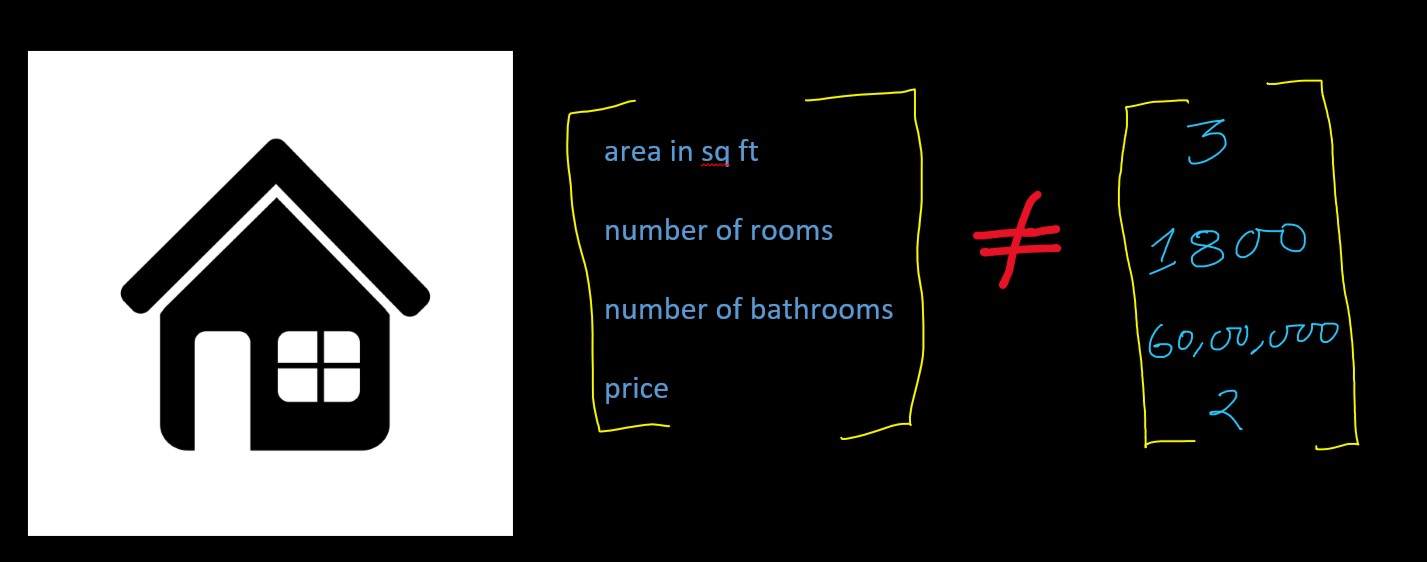
Vectors: In field of computer science, Vectors are ordered list of numbers, sometimes
also refered as array or lists. Vectors are called as Ordered list because, Order
of the elements in the list matters. E.g. if we have a vector representing the attributes of
a house, i.e.
- area in square feet
- number of rooms
- number of bathrooms
- price of the house
then it can be represented as:

However, if we were to not follow a order, while writing the elements of our house vector, than the representation and meaning that is held by our house-vector, to represent some values or attribute of a house breaks and makes no practical sense. E.g.
Also, in mathematics Vector could be anything that satisfies the notion of addition and/or
multiplication
Vector has a tail, a head & the co-ordinates, i.e. how to reach from tail
to its head.
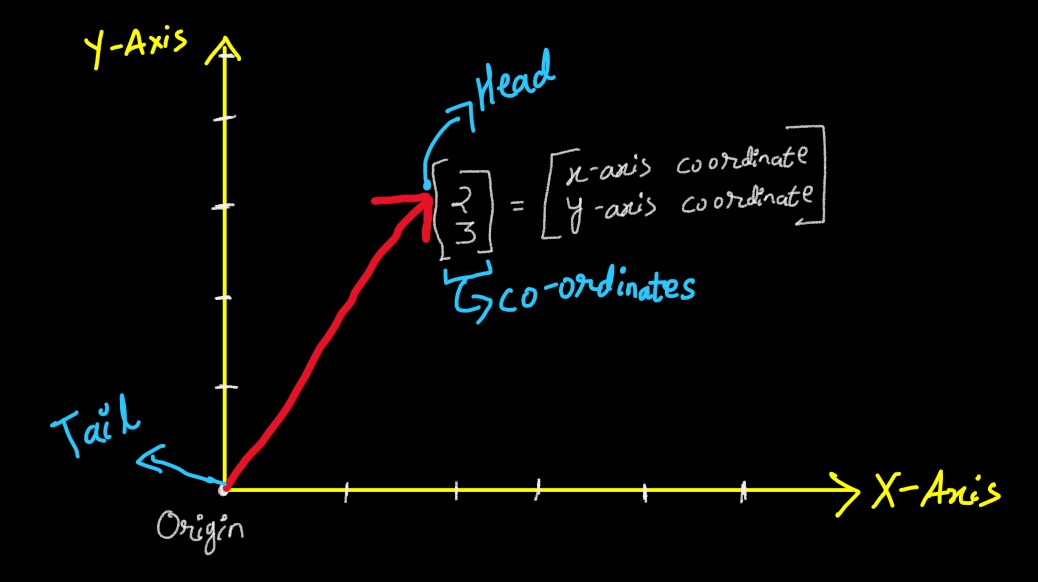 I.e. Co-Odrinates are simply the way to reach the head of the Vector, i.e.
I.e. Co-Odrinates are simply the way to reach the head of the Vector, i.e.
 So, we will first move 2 point on x-axis, and then 3 point on y-axis, to reach
from tail to head of a vector
So, we will first move 2 point on x-axis, and then 3 point on y-axis, to reach
from tail to head of a vector
Lets suppose we have 2 vectors, a
⃗ &
b ⃗ ( vectors are denoted by
→
over thier name ), with following co-ordinates in a space:
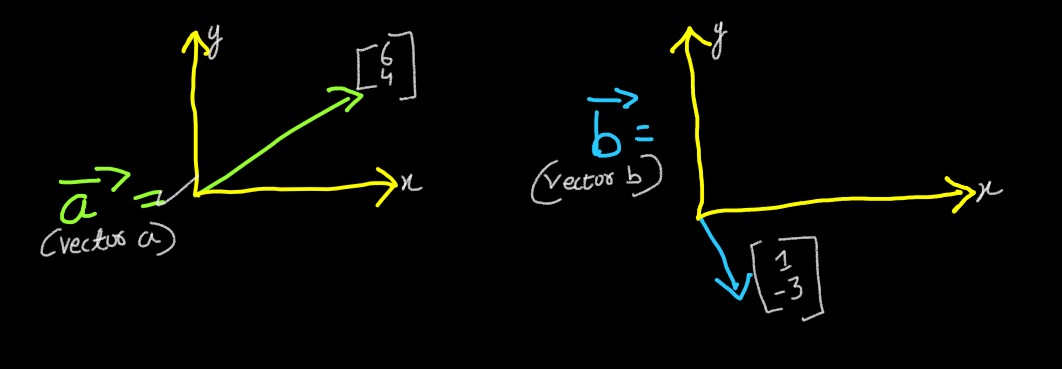
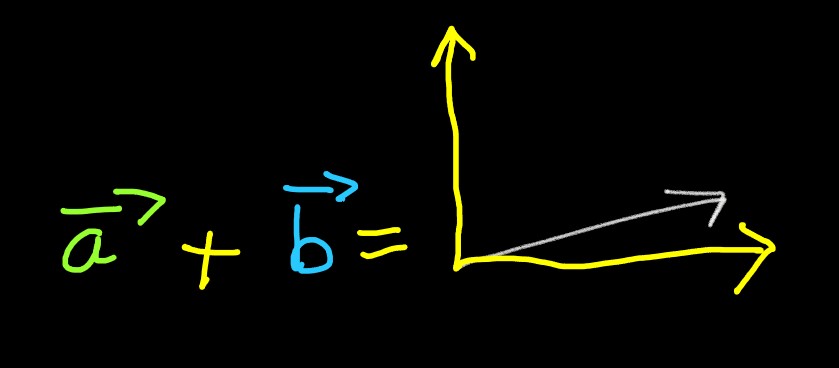
Being able to add 2 vectors would mean, lets suppose you had to walk a path, then walking the
path in vector a means walking from the tail of vector a to it head. And similarly
for vector b.
However, addition of a ⃗ &
b ⃗ , you have to walk from
tail of a ⃗
to its top, and from its top begins the tail
of b ⃗ , and you have to walk from tail
of vector b to top of b ⃗ , which could
be symbollically be represented as:
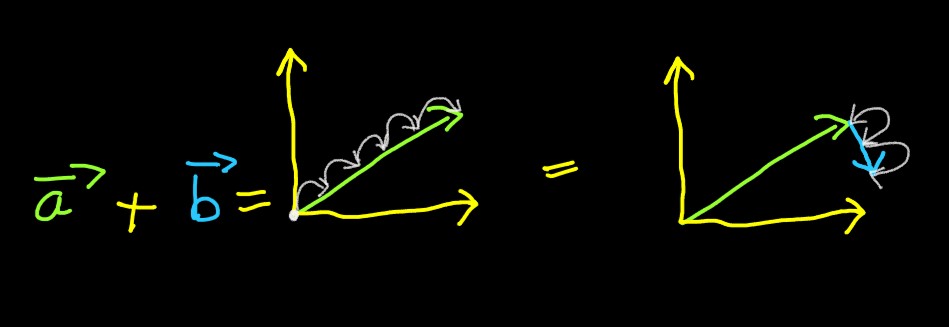
Another way of depicting the final destination of the above formed path would be:
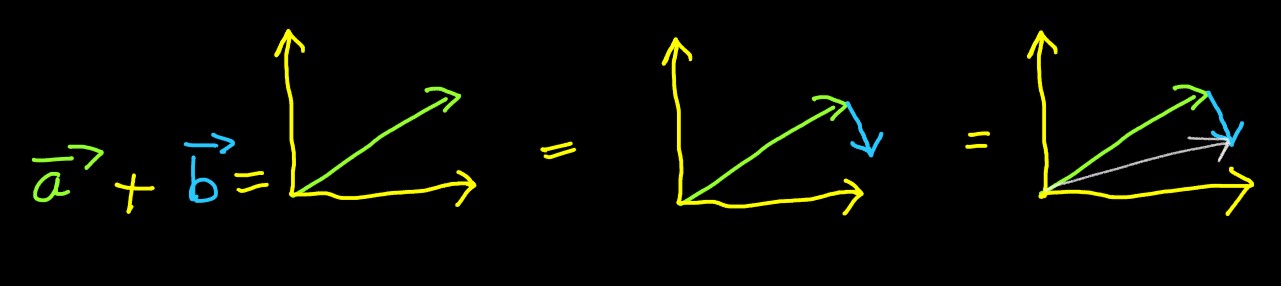
Thus, the shortest path from the source (usually origin, or the point where x-axis
and y-axis interesect) to destination is the addition of a
⃗ and b
⃗
can be represented directly as:
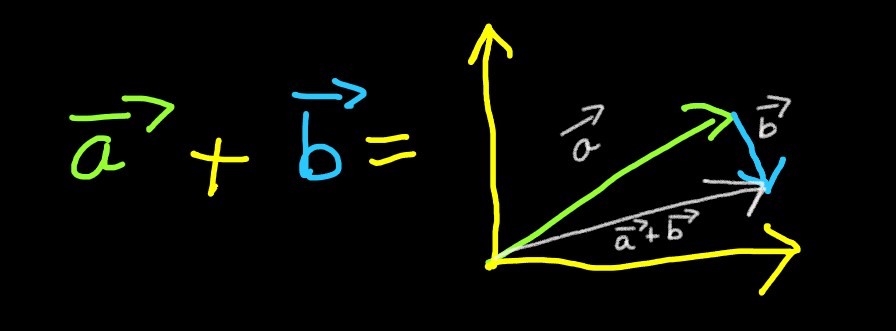
Or simply:
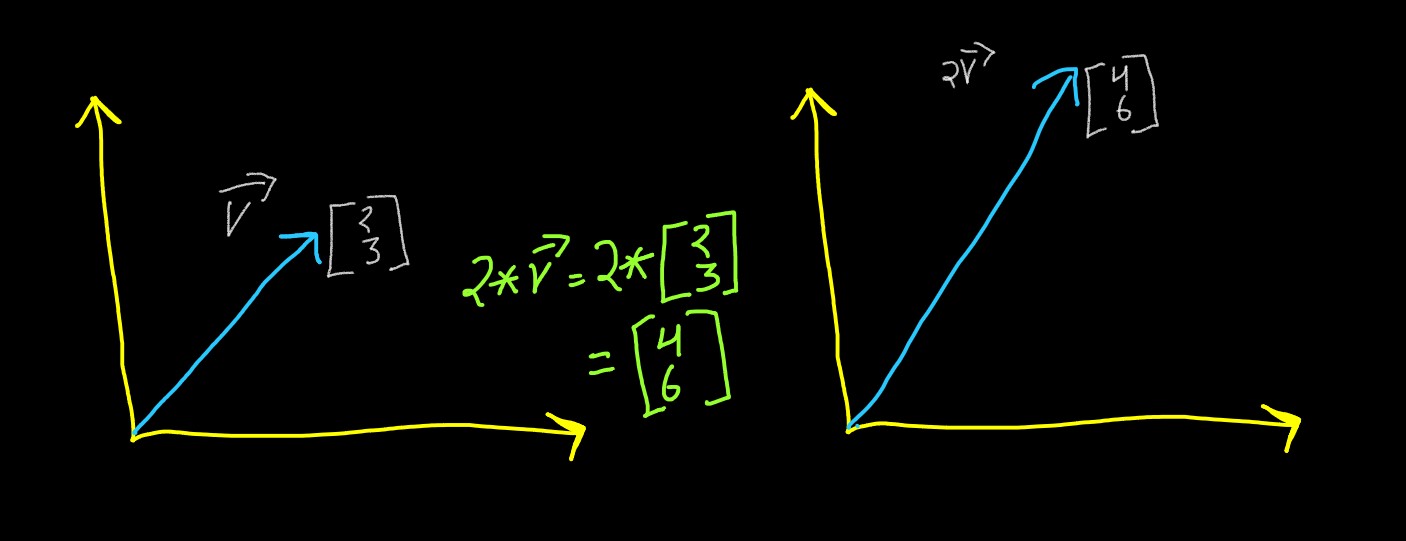
Other than Addition, Vectors also support Multiplication. Vector multiplication are
equivalent to Stretching or Shrinking of vectors, e.g. if we have a v⃗
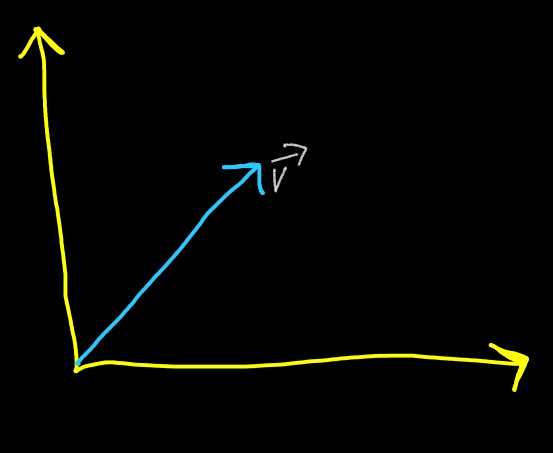
And we multiply v⃗ with 2,
the vector gets transformed to
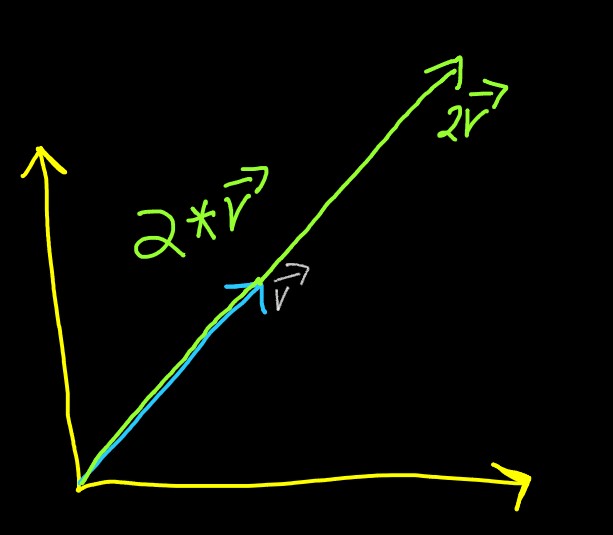
Here, the vector has been stretched to become twice of its actual size as it was multiplied by
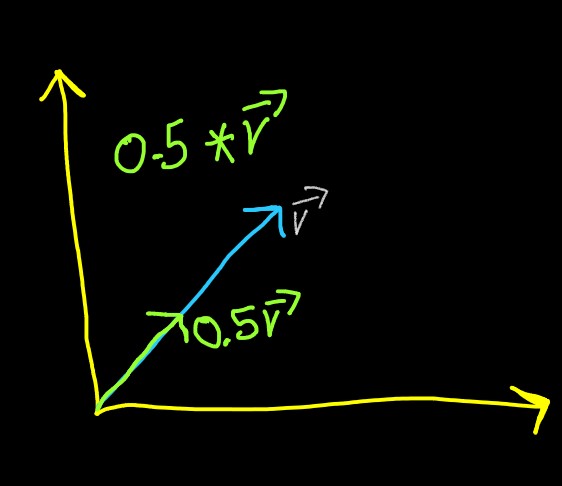
2. Similar thing will occur if the same vector get multiplied by 0.5, i.e. it becomes half of
its original size (shrinks)
But what happend if the vector is multiplied by a negative number? First it will get flipped, as
the sign is negative, and then it will get multiplied by the number
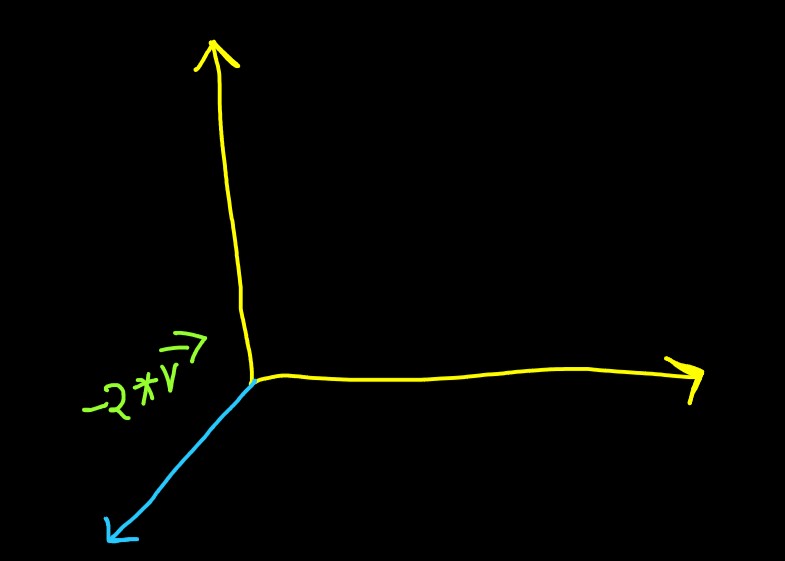
This process of stretching and shrinking of vectors is called as Scaling, and the number
used to perform the scaling operation is called as Scalers, i.e. 2 or 0.5 in above
example.
Mathematically, the Scalers and the operation of Scaling is expressed as
System of Linear Equations
Fundamental problem of Linear Algebra: Solve a system of Linear Equations

This equation can be broken down into:
- Matrix of Coefficients
- Vector of Unknowns
- Result Vector
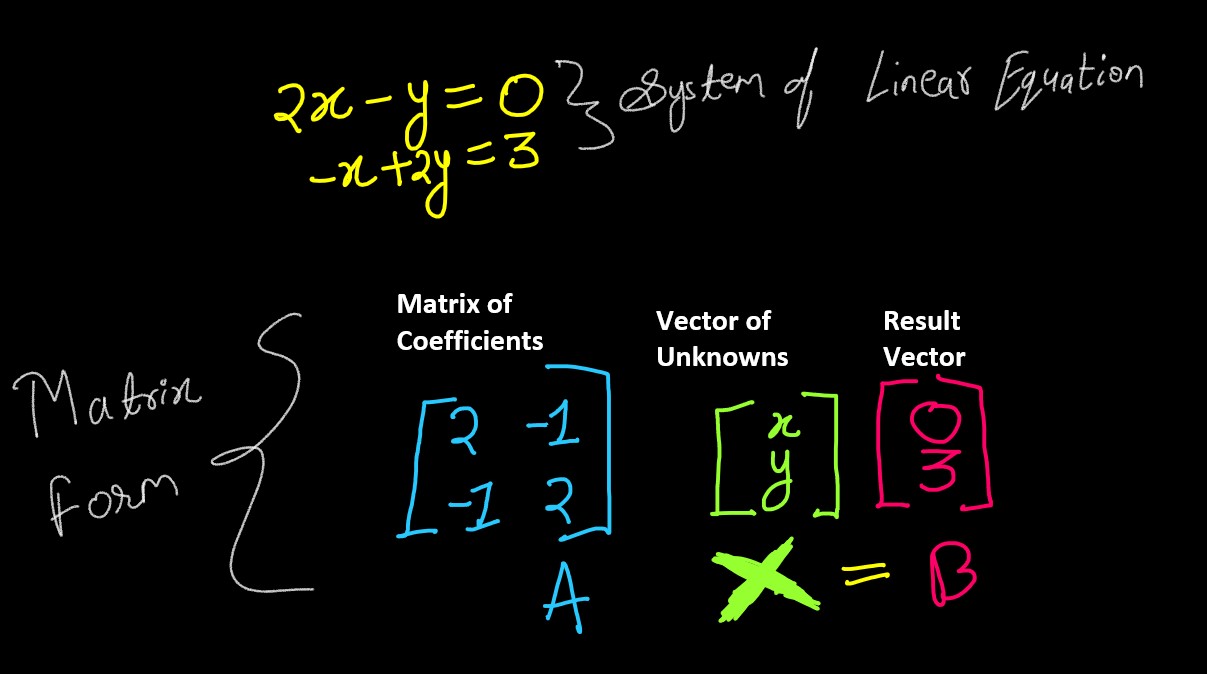
We're interested to work on System of Linear Equation because we want to find the Solution of System(Vector of Unknowns in above picture), i.e. what satisfies the system (set of Equation).
